九州大学青木研究室-理論化学グループ
　　　　　Elongation法


●はじめに●

　近年、量子化学計算は急速に発展を遂げたといっても、小さな分子に対してだけで、（生体）高分子等巨大系に対しては未だ無力である。実際に、材料開発の観点から分子設計を行い、また生体高分子における機能や役割を解明するためには、古典力学に基づくシミュレーションではなく、高精度な量子化学計算で電子状態を知ることが最終的な目標になると思われる。なぜなら、導電性や磁性あるいは生体内協同現象などは、マクロな立場で解明できる範囲にはなく、原子・分子レベル、つまり行き着くところはミクロな電子論的な性質に基づいているからである。これらのことから、巨大高分子系に対して、その電子状態を効率良く、しかも高精度で求める方法論を確立することは必須と思われる。

　そこで、高分子や結晶に対して行っていた当グループ独自のアプローチの中で、以前より発展させてきたElongation法をはじめ、特に有用だと期待できるいくつかの方法論を融合させることにより、機能性高分子のための分子設計システムの開発を行う。本方法は巨大系に対する効率的な計算手法として一般的な方法であるため、目的とする系や物性によってElongation法そのものの計算手法が変更することはない。よって、高分子系一般に対する効率的計算手法として発展させたあとに、目的とする個々の物性に応じて、それぞれ独自の計算ルーチンをプログラムに盛り込んでいく必要がある。

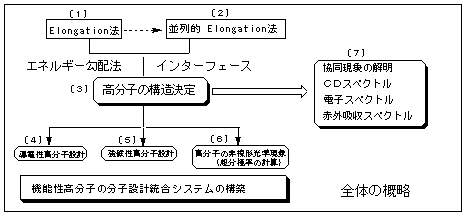
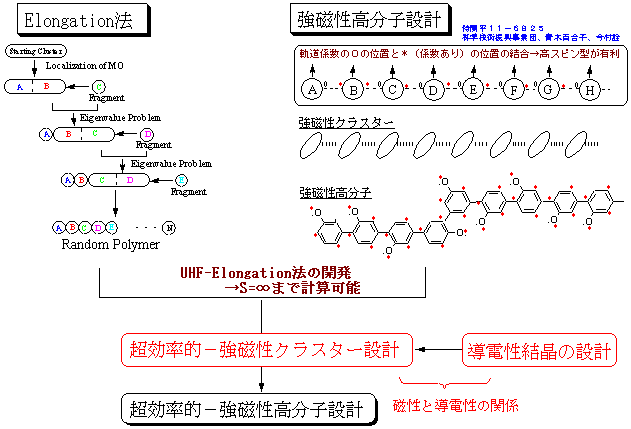
　本計画の概略は下図のように表されるが、「Elongation法」および「並列的Elongation法」の開発の他、現在までに既に何らかの形で関わってきたものに、「導電性高分子の設計」、「強磁性高分子の設計」および「高分子の非線形光学現象」がある。それぞれ新規なアイデアを提出し、特許を申請中あるいは論文投稿中の段階であり、未だ開発途中の段階である。これらをElongation法と結合させることにより実用化していきたい。下図において、太枠で囲ったものはこれから新しく計画する部分であるが、それ以外については、現在開発段階あるいはほぼ見通しのついたものもある。各項目は〔１〕－〔７〕でそれぞれ説明する。

　

 〔１〕Elongation法の経験的および非経験的分子軌道法のレベルでの確立

　Elongation法とは、図Ａに示すように、小さなオリゴマーを出発クラスターとして、高分子の重合反応を追跡するようにしてフラグメントを順次付加させながら、高分子鎖の電子状態を求めていく方法である。本方法では、図Ｂに示すように、クラスター側の分子軌道を付加するフラグメントから離れた局在化軌道(Frozen LMO)とフラグメントに近い局在化軌道(Active LMO)に分け、フラグメントは、Active LMOとのみ相互作用させる。よって、高分子鎖にフラグメントを付加させる度に、高分子鎖側の反応末端と付加するフラグメントの間の局所的な相互作用のみを取り扱うため、全系をまともに扱う従来の計算に比べて、極めて効率よく電子状態を求めることができる。また、Frozen LMOは、フラグメントとの相互作用がある閾値以下になったら計算からはずすようにしているため、計算精度を落とすことなく、正確にかつ効率的に高分子鎖の電子状態を合成していくことができる。本方法は、どのようなランダム系に対しても適用可能である。

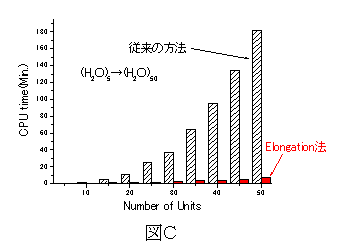
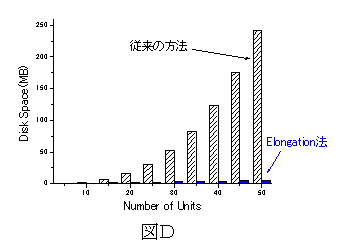
　図Ｃには、密度汎関数法のレベルで、水クラスターを５個から５０個まで伸長していく過程で必要な計算時間を、全系をまともに取り扱う従来の方法と、Elongation法との比較で示す。図Ｄには、計算に要する２電子積分の保存のために要するディスク容量を、従来の方法と、Elongation法との比較で示す。

　

 〔２〕並列的Elongation法の開発-〔１〕で開発した逐次的Elongation法に対して並列処理を導入

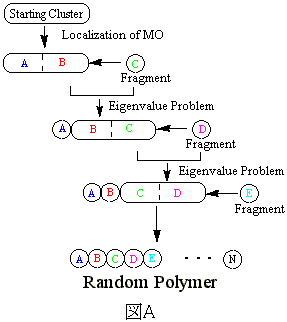
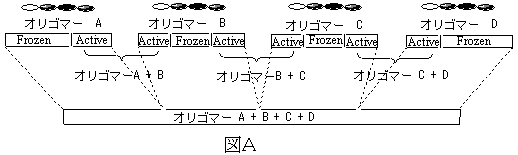
　目的とする高分子鎖をｍ個に切断し、それぞれの末端を水素原子でキャップすることによりｍ個のオリゴマー分子を作成し、それぞれを、逐次的Elongation法を用いて電子状態を計算しておく。

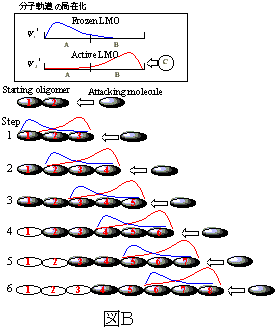
　その結果、オリゴマー鎖の各セグメント上に局在化したLMOが形成されているため、オリゴマー間の結合に際して強く相互作用する部分に局在化した活性局在化分子軌道（ActiveＬＭＯ）と結合に関与しない不活性局在化分子軌道（FrozenＬＭＯ）に分ける。その後、図Ａのように、同時にそれらオリゴマー間の電子状態間を並列分散処理により合成することによって、巨大高分子系の電子状態を一度に求める。

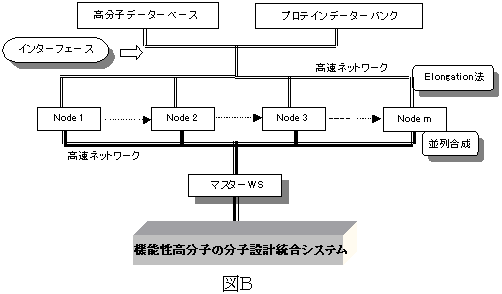
　本方法の並列分散処理のハードウエア構成図は，図Ａに対応して図Ｂのようになる。それぞれのオリゴマーを伸長する際には高分子の原料となるモノマーに関するデータベースから選択し、それぞれのデータを合体相手のオリゴマーの計算結果の存在するNodeに転送して固有値問題を解く。

　

 〔３〕高分子の構造決定

　〔１〕と〔２〕で開発したElongation法および並列的Elongation法にエネルギー勾配法を導入し、高分子鎖の効率的構造最適化計算を可能とし、構造転移における協同現象の解明を行う。

　

 〔４〕導電性高分子・擬一次元導電体の設計

　周期性高分子のみならず、高分子の末端制御による導電性の増大、ドーパントの存在下における導電性の増大等、高分子に非周期性が加わった場合に対して、Elongation法は強力な計算道具になる。さらに、TTF-TCNQなど、電荷移動錯体からなる導電性結晶のパイエルス不安定性に関して、既に解析的なアプローチを提出してきた。このアプローチによって設計した擬一次元導電性結晶が実際に導電性を有するかどうかについて、従来の全系を計算する方法では確かめることは不可能であるため、Elongation法によって検証していく。

　

 〔５〕強磁性高分子設計

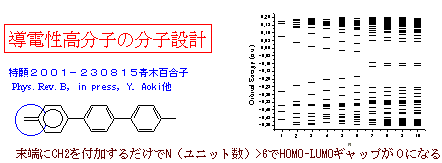
　有機強磁性高分子の設計として、簡単な規則によって分子間を結合させると強磁性的になることを示し、既に特許を取得している。これは、右上図のように、「分子間の結合において、分子軌道係数の０の部分と何らかの値のある＊の部分で結合させると、高スピン型が有利となる」というシンプルな規則で、数学的にも既に証明済みである。これにより種々の有機強磁性高分子として期待されるものを設計し、その高スピン度を定義する方法も提出した。しかし、このようにして設計した高分子が、果して現実に強磁性を示すのかを、全系をまともに扱う従来の計算方法で確認するのは困難であった。そこで、Elongation法によって、末端のみを高スピン型で繰り返し解いてＳ＝∞まで計算する方法を既に開発している。これを発展させて、種々のスピン多重度に対しても容易にElongation法が適用できるようにし、有機強磁性高分子の設計のための道具として開発していきたい。

　

 〔６〕高分子の非線形光学現象

　分子の非線形光学現象である超分極率を求める方法としては、Coupled-Perturbed-Hartree-Fock(CPHF)法と、Finite Field(FF)法が存在する。しかし、両方法とも小さな分子ですら膨大な計算時間を要し、共役高分子系におけるPush-Pull系等の非周期性高分子に対して、全系の（超）分極率を求めることは不可能である。 そこで、これらの方法をElongation法に組み込み、効率的に超分極率を求めることが可能となるよう発展させている途中である。Table I に、Finite Field(FF)－Elongation法によるポリエチレン(n=20→23)の超分極率をElongation法(上段)と従来の方法（下段）の比較で示す。

　

 〔７〕協同現象の解明

　生体高分子やポリシラン誘導体で実験的に観測されている協同現象について、 すでに理論計算からも興味深い知見を得ている。構造最適化Elongation法を、 特に生体機能と協同現象の関連に応用したい。

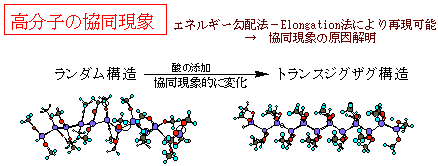
　Elongation法によるポリシラン誘導体のプロトン化による協同的構造変化への 量子化学的アプローチの例
Elongation法によってシランオリゴマーの合成H(SiR2) 12 + (SiR2)6 Hを繰り返し行うが、 R=OCH3の場合に得られた計算結果から一般的に言えることを以下にまとめる。まず、出発 クラスターH(Si(OCH3)2) 12 Hはプロトン化によりトランス構造になる。次に、攻撃分子である (Si(OCH3)2) 6 Hを結合すると
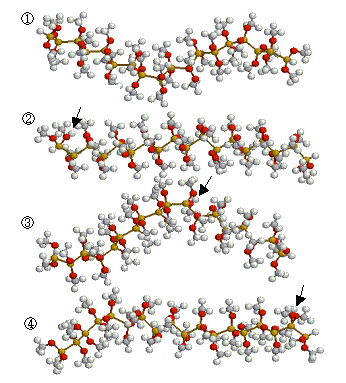
(1)プロトンが付加しない場合は、初期構造よりはトランスに近いランダム構造が得られる。
(2)左末端をプロトン化すると、プロトン近傍がトランス構造に近くなる。
(3)真中付近をプロトン化すると主鎖が折れ曲ることが多く、それぞれの部分は、大体トランス構造になっている。
(4)右末端をプロトン化すると、プロトン近傍がトランス構造に近くなる。
これらのことから、プロトンそのものの効果は12－14ユニットほどに広がっていることが示唆される。 プロトン数を増やしたときの効果や、波動関数の局在性と協同現象との関連について現在解析を行っている。

| Topページへ | Back |