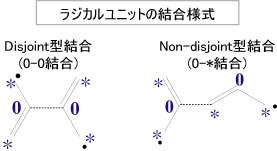（補足“Non-disjoint型におけるNBMOの保存”） ･････････････････････････････････････････････････････････････････････････････････････････ 図１　　　 　まずは、アリルラジカル２分子のDisjoint型(0-0)結合モデル(図１ 左)についての永年方程式（分子軌道ベース）を式１に示した。行列式の左上３行３列はDisjoint型の左側のユニット分子に、右下３行３列は右側のユニット分子に相当する．左下および右上領域はユニット間の相互作用に対応する．ε2（=α）は孤立したアリルラジカルユニットのNBMOの軌道エネルギーである．行列式から明らかなのは、NBMOに関する非対角項要素がすべてゼロになることである。この行列式はすぐに(ε2-ε)2×(行列式')の形に変形でき、２つのNBMOのエネルギーレベルが保存される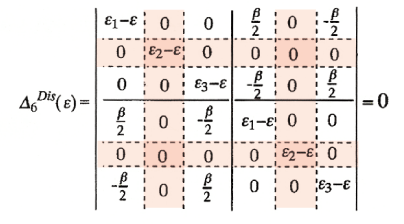． 式１　　　 　次に、Non-disjoint型(0-*)結合モデル(図１ 右)についての永年方程式を式２に示した。左側ラジカルユニットについてはNBMOが保存される一方で、右側ユニットではβ/2と-β/2の相互作用が生じている。しかしここで、pairing theorem（ε-ε1=ε3-ε）が成立するとしたとき、最終的に式３のように(ε2-ε)2=(α-ε)2を取り出すことができるため，Non-disjoint型(0-*)でも２つの縮重したNBMOが得られる。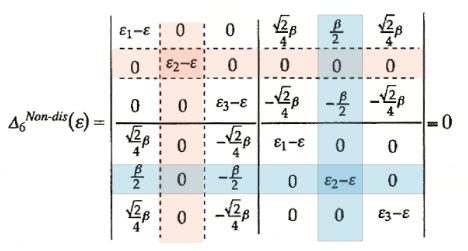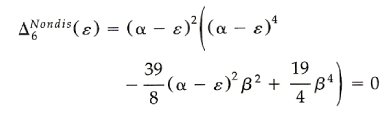 式２　　　 式３　　　 　このように、Disjoint型(0-0) および Non-disjoint型(0-*)の結合様式で縮重NBMOが得られることを"変分的に"証明した。 【参考文献】　Y. Aoki, A. Imamura, Int. J. Quantum Chem., 74, 491(1999). ･････････････････････････････････････････････････････････････････････････････････････････